
Apply the transformations in this order: 1.

Then compose a sequence of transformations that will transform the graph of y f ( x) into the graph of. A function presented in tabular form can also be reflected by multiplying the values in the input and output rows or columns accordingly. Apply the following steps when graphing by hand a function containing more than one transformation. In Exercises 69, first write g ( x) in terms of.The order in which the reflections are applied does not affect the final graph. A graph can be reflected both vertically and horizontally. Graph transformations Given the graph of a common function, (such as a simple polynomial, quadratic or trig function) you should be able to draw the graph of its related function.A graph can be reflected horizontally by multiplying the input by –1. We input a value that is 3 larger for g\left(x\right) because the function takes 3 away before evaluating the function f. To get the same output from the function g, we will need an input value that is 3 larger. Given a square root function or a rational function, the student will determine the effect on the graph when f(x) is replaced by af(x), f(x) + d, f(bx). For example, we know that f\left(2\right)=1. The steps below will help you identify if the shown transformation is. Translate 5 units in the positive Y directionĬf(bx+a)+d = Translate by a units in the negative X direction, then scale by a factor of 1/b parallel to the X-axis, then scale by a factor of c parallel to the Y-axis, then translate by d units in the positive Y direction.Ĭ+d = Scale by a factor of 1/a parallel to the X-axis, then translate by b units in the negative X direction, then scale by a factor of c parallel to the Y axis, then translate by d units in the positive Y direction.The formula f\left(x\right)=f\left(x - 3\right) tells us that the output values of g are the same as the output value of f when the input value is 3 less than the original value. Identifying Transformations on a Graph The three transformations we will look at are rotations, reflections, and translations.

Graphing transformations of this type involves creating a table of the original and the. Scale by a factor of 3 parallel to the Y axis One of the most basic types of transformations is y af(x) + b. Hence, we need to translate x 3 one unit to the right and one unit downward. Solution Let’s break down h (x) first: h (x) (x 1) 3 1.
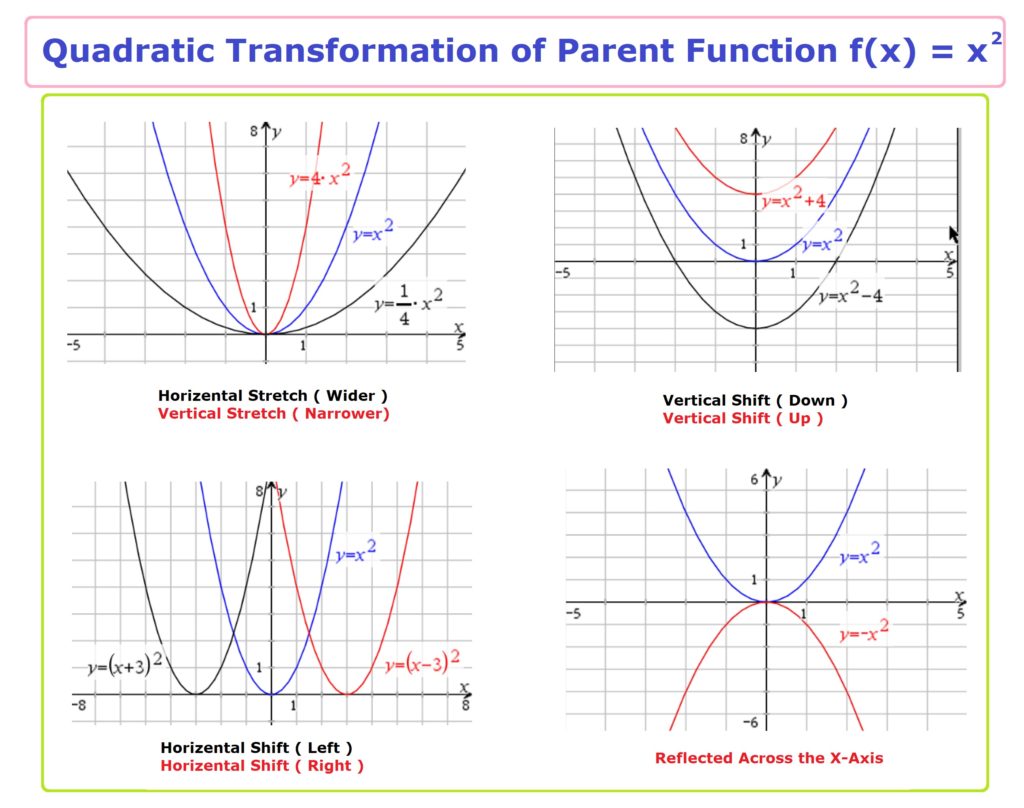
Scale by a factor of 1/2 parallel to the X axis Use the transformations to graph h (x) as well. Translate 4 units in the positive X direction So scale parallel to the X axis by a factor of 1/2, then move left by 2 units. Hence, the original point becomes x= (8/2)-2 = 2ĭescribe the transformation of 3f(2x-4) + 5. If we want to do scaling first, we need to factorise into f 2(x+2).
GRAPH TRANSFORMATIONS SERIES
Hence, the original point becomes x= (8-4)/2 = 2 This series of lessons/project involves parent graphs and transformations for linear, quadratic, absolute value, square root, circular, exponential and. Move left by 4 units, then scale parallel to the X axis by a factor of 1/2. Let’s look at this example to illustrate the difference:įor f(2x+4), we do translation first, then scaling.

Knowing whether to scale or translate first is crucial to getting the correct transformation. s e We can obtain the graph of y a f (b x + c) + d by starting with the graph of y f(x) and transforming each point as follows. Visit Maths.scot for notes and worked examples for every Higher Maths topic.
GRAPH TRANSFORMATIONS FREE
In the transformation of graphs, knowing the order of transformation is important. Higher Maths: Graph Transformations This resource is free to distribute and use on a non-commercial basis.


 0 kommentar(er)
0 kommentar(er)
